AlgoDat SoSe2000, Aufgabe 65
Christian Semrau

a, b) Bildliche Darstellung ohne gekreuzte Kanten:

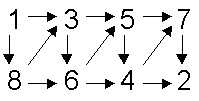
c) Kantenliste:
8,13, 1,3, 1,8, 3,6, 3,5, 4,2, 4,7, 5,4, 5,7, 6,4, 6,5, 7,2, 8,3, 8,6

d) Knotenliste:
8, 2,3,8, 0, 2,5,6, 2,2,7, 2,4,7, 2,4,5, 1,2, 2,3,6

e) Adjazenzmatrix:

	1	2	3	4	5	6	7	8
1	0	0	1	0	0	0	0	1
2	0	0	0	0	0	0	0	0
3	0	0	0	0	1	1	0	0
4	0	1	0	0	0	0	1	0
5	0	0	0	1	0	0	1	0
6	0	0	0	1	1	0	0	0
7	0	1	0	0	0	0	0	0
8	0	0	1	0	0	1	0	0

f) Adjazenzliste:

1	3, 8
2
3	5, 6
4	2, 7
5	4, 7
6	4, 5
7	2
8	3, 6

Kantenliste realisiert als int[], wobei der Index 0 die Knoten, der Index 1 die Kanten zählt, die übrigen Elemente sind (in Paaren zusammengefasst) die Kanten.
Knotenliste realisiert als int[], Index 0 speichert die Knotenanzahl, danach die ausgehenden Kanten jedes Knoten entsprechend der Nummerierung, indem erst die Anzahl der Kanten und dann die Zielknoten angegeben werden.
Die Realisierung als LinkedList ist in beiden Darstellungen günstiger (verbessert Einfügen und Löschen, ändert nichts an der Suchdauer).

Adjazenzmatrix realisiert z.B. als int[][], wobei die Größe in beiden Indizes der Knotenanzahl entspricht. Das Element [i][k] gibt an, ob eine Kante von Knoten i zum Knoten k führt (Werte 0 oder 1).

Adjazenzliste realisiert z.B. als LinkedList[] (ermöglicht direkten Zugriff auf die einzelnen Listen). Jede Liste speichert die Zielknoten ausgehender Kanten eines Knoten. Eine andere mögliche Implementierung, die einzelne Operationen beschleunigt, ist ein Array von sortierten Binärbäumen (ermöglicht logarithmischen Aufwand bei Kantenoperationen).